Punto
El punto es una figura geométrica adimensional: no tiene longitud, ni área ni volumen, ni otro análogo dimensional. No es un objeto físico. Describe una posición en el espacio, determinada respecto de un sistema de coordenadas preestablecido.
Linea
En geometría, una línea es una sucesión continua de puntos infinitos. Es una figura geométrica que sólo tiene una dimensión: longitud.
Puntos Colineales
Puntos que están sobre una misma recta.
Angulo
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen. Suelen medirse en unidades tales como el radian, el grado sexagesimal o el grado centesimal.
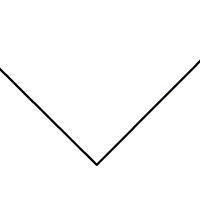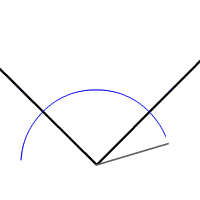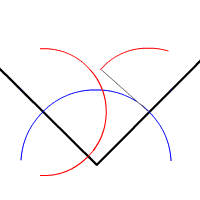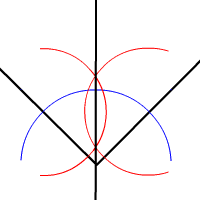
Bisectriz
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirrectas de un ángulo.
Polígono
Un polígono es una figura geométrica formada por segmentos consecutivos no alineados, llamados lados.
Los polígonos cuyos lados no están en el mismo plano, se denominan polígonos alabeados.
Circunferencia
A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia.
Angulo Central
Es un ángulo cuyos lados son radios y su vértice es el centro de la circunferencia.
Arco
Es cualquier curva contínua que une dos puntos.También, se denomina arco a un segmento de circunferencia; un arco de circunferencia queda definido por tres puntos, o dos puntos extremos y el radio, o por su cuerda.